Concepto de axioma

La palabra axioma procede etimológicamente del griego, siendo derivada del verbo αξιοειν o “axioein” cuyo significado puede traducirse como valorar como auténtico, justo y claro. Una proposición puede ser considerada axioma cuando su verdad resulta evidente sin que sea necesario demostrarla, y sobre esa base se van construyendo las teorías científicas.

Se usa además, especialmente en Lógica y en Matemática. En Lógica son axiomas, palabra ya usada por el filósofo griego Aristóteles, las proposiciones que se usan como reglas o punto de partida, no resultando derivadas de otras, sino que otras proposiciones se derivan de ellas, pues se aceptan por ser evidentes y necesarias, siendo su demostración o bien imposible o de lo contrario, inútil, pues de negarlas se produciría una contradicción, como sucedería si tratáramos de negar que todo individuo es igual a sí mismo. Un claro ejemplo de axioma es el sentado por Descartes “Pienso, luego existo”.

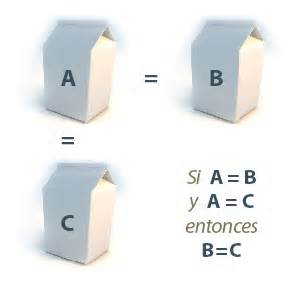
Los principios básicos de la matemática fueron llamados axiomas en la modernidad por el filósofo Immanuel Kant, llamándolos juicios sintéticos a priori, porque se descubren intuitivamente antes de la experiencia. Ejemplo de axioma matemático: “dos cantidades que son iguales a una tercera cantidad, resultan a su vez, iguales entre ellas”.

En Geometría, los axiomas son proposiciones que surgen de relacionar el punto, la recta y el plano (geometría euclidiana). El matemático de origen alemán, David Hilbert (1862-1943) creó un sistema de axiomas, basado en nueve nociones (el punto, la línea, la recta y el plano) y seis relaciones (una de orden, tres de pertenencia y dos de congruencia) que consideró “primitivas”.

Fingermann, H. (1 de agosto de 2013). Concepto de axioma. Deconceptos.com. https://deconceptos.com/general/axioma