Concepto de números primos

Los números primos son aquellos que solo resultan divisibles por sí mismos y por la unidad. Los que pueden dividirse por otros números, se denominan compuestos (por ejemplo el 9 que además de dividirse por 9 y por 1, también puede dividirse exactamente por 3). Fueron ya conocidos en la antigüedad por la civilización griega, habiendo sido usados por Euclides, quien demostró que poseen la particularidad de ser infintos. El número 1 no integra ninguna de las dos categorías, por convención, a partir del siglo XX, y por supuesto solo es divisible por sí mismo al ser él mismo la unidad.

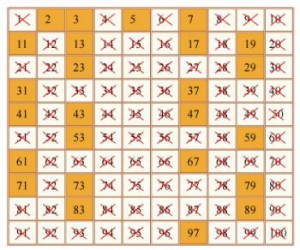
Son por ejemplo números primos el 2, el 3, el 5, el 7 y el 11. El número 2 es el único número primo par. Tienen la característica de ser números enteros y positivos.

Para indagar si un número es primo se debe buscar si existe algún número que pueda dividirlo exactamente, y será primo si ese número solo es él mismo o la unidad. En la actualidad son usados ordenadores para determinar si un número es primo.

Un número entero puede descomponerse en sus factores primos, y ello se logra al expresarlo como producto de números enteros, todos ellos primos, hallando los divisores del número tomado en consideración. Habitualmente se colocan debajo del número a descomponer el número resultante de dividirlo por los números primos divisores, hallando así cocientes parciales, colocados a la izquierda de los divisores. Cuando el cociente ya no admite más divisores que el propio número y la unidad, la descomposición finaliza.

Fingermann, H. (30 de mayo de 2011). Concepto de números primos. Deconceptos.com. https://deconceptos.com/matematica/numeros-primos