Concepto de hipérbola

La palabra hipérbola es un sustantivo femenino, de uso en Matemáticas y Geometría que se originó en el griego ὑπερβολή (léase hyperbolē) vocablo compuesto de ὐπέρ o “hyper”, en el sentido de “sobre” o «encima» y por βάλλω o “ballō”, verbo que se traduce como «lanzar”, pasó al latín como “hyperbŏla” y de allí fue tomada por el español. Su significado literal es “ir más allá” o “exagerar”.

Estudiando la duplicación del cubo, el matemático griego Menecmo que vivió en el siglo IV antes de Cristo descubrió las secciones cónicas, al cortar una parábola con una hipérbola, pues se logra al cortar un plano recto con un plano que resulta oblicuo al eje. El primero en usar el término fue Apolonio de Perge (262 a. C-190 a. C) autor de “Sobre las secciones cónicas” que también acuñó los términos elipse y parábola.

Estos estudios se complementaron por el filósofo modernista René Descartes quien en su obra “El discurso del método” publicado en 1637, trata la hipérbola entre las secciones cónicas.

Entendemos por cónica el conjunto de puntos ubicados en un plano de referencia que se caracterizan por la proporción constante e igual a “e” (excentricidad) entre su distancia a un punto “f” (foco) y a una recta D, denominada directriz. En la hipérbola el parámetro “e” es mayor que 1. Si fuera menor que 1, se trataría de una elipse.

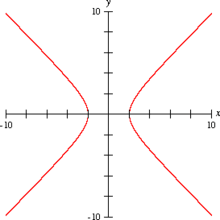
En un plano, la hipérbola es una curva abierta que posee dos ramas y dos puntos fijos llamados focos, con respecto a los cuales, todos los puntos de la curva conservan igual distancia o distancia constante. Además de los focos, son elementos de una hipérbola, el centro (punto donde se produce la intersección de los ejes) los vértices (puntos donde se da la intersección del eje focal con la hipérbola) y el eje focal (recta que pasa por los dos focos). El elemento que distingue a la hipérbola de otras cónicas son las asíntonas, rectas de ecuaciones que se acercan a la curva, pero no la alcanzan.

Fingermann, H. (26 de noviembre de 2019). Concepto de hipérbola. Deconceptos.com. https://deconceptos.com/matematica/hiperbola