Concepto de polinomio

La palabra polinomio, tiene su origen en la unión de dos términos griegos; “polys” que significa “muchos” y “nómos” en el sentido de regla; pasó al latín como “polynomium” y de allí al español, siendo usada en matemáticas, desde muy antiguo, pero desarrollado el concepto, especialmente desde el siglo XV, para designar a aquella suma algebraica compuesta por una serie finita de monomios, entendiéndose por monomio, a la expresión algebraica que es entera, y tiene un solo término, por ejemplo, 5ax².

Aclaremos que una expresión algebraica es el conjunto de números y símbolos expresados en letras, que están enlazados entre sí por signos matemáticos, indicativos de la operación que se debe efectuar.

Volviendo al polinomio, puede tener solo dos términos, en cuyo caso, se denomina, binomio.

Se dice que un polinomio está ordenado cuando sus grados están escritos de modo creciente o decreciente, siendo el grado de un polinomio, el término de mayor grado. Tras efectuar las operaciones indicadas, se obtienen los valores de las letras o incógnitas, y ese es el valor numérico.

Ejemplo de polinomio: P(x) = 2x^4+ 4x^2 + 5x – 4

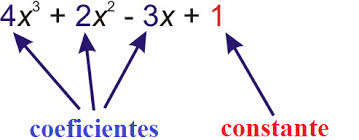
En este ejemplo, la variable (también llamada indeterminada, de la que debemos descubrir su valor es x, siendo los coeficientes (números que van situados a la izquierda de la variable o indeterminada) 2, 4 y 5; siendo -4, el término independiente. El coeficiente principal del polinomio es el último término, no nulo, de la sucesión dada.

Si efectuamos la suma de dos polinomios se obtiene otro polinomio con coeficientes iguales a los coeficientes de los sumados, en forma ordenada. Para sumar o restar los polinomios, deben agruparse los términos (que están separados por los signos de + y de -) y simplificarse los monomios que sean semejantes. En caso de querer multiplicarlos. se debe multiplicar cada término de un polinomio, por cada uno de los términos del otro, simplificándose, después, los monomios que sean semejantes.

El desarrollo de la informática ha sustituido los polinomios por funciones “spline”, que son más flexibles, en muchos casos. Una función “spline”, se forma con varios polinomios, estando definido, cada uno, sobre un subintervalo, produciéndose la unión de acuerdo a determinadas condiciones de continuidad.

Fingermann, H. (10 de septiembre de 2021). Concepto de polinomio. Deconceptos.com. https://deconceptos.com/matematica/polinomio