Concepto de conjunto

Se denomina conjunto a la agrupación de entes o elementos, que poseen una o varias características en común. Un conjunto, es un concepto intuitivo empleado en matemática, que elaboró la teoría de conjuntos. Para saber si un conjunto está bien definido habrá que atender a la siguiente regla: cuando la pertenencia de un elemento a un conjunto es clara, el conjunto estará bien definido. Por ejemplo, nadie dudaría de incluir al Domingo entre los días de la semana, pero el conjunto de personas rubias no está bien definido, pues hay dudas si determinadas personas pertenecen o no al conjunto, pues la calidad de rubio no es precisa.

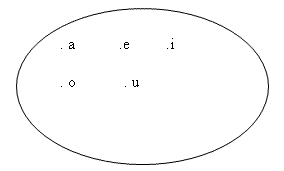
Un conjunto es representado por una letra mayúscula, encerrándose sus elementos, separados por comas, entre llaves. Por ejemplo, el conjunto A, integrado por las vocales, se representaría así: A= {a, e, i, o, u}

Gráficamente se utiliza el diagrama de Venn, en homenaje a su creador, el británico John Venn, que son líneas circulares u ovoides cerradas, donde se disponen los elementos, señalados mediante puntos. El conjunto A mencionado quedaría representado así:

Si definimos un conjunto por extensión, debemos enumerar cada uno de sus elementos. En el caso de las vocales, se deben nombrar todas ellas: a, e, i, o, u, como lo hemos hecho anteriormente. Si lo definimos por comprensión nombramos solamente la propiedad o característica que los aglutina. En el mismo caso diríamos A= {las vocales} o A= {X/X es una vocal} que corresponde leer: A es el conjunto de X, tales que X es una vocal.

Los conjuntos complementarios son aquellos formados por todos los elementos de uno que no pertenecen al otro. Dados dos conjuntos, uno A, formado por los siguientes alumnos de un colegio, de cuarto grado B {Juan, Alfredo y Jesús} y otro conjunto B formado por alumnos de cuarto grado en general { Juan, Alfredo, Jesús, Diego, Victoria y María} el conjunto complementario estaría formado por Diego, Victoria y María.

Se dice que un conjunto A está incluido en otro B, cuando todos los elementos de A pertenecen a B. En el ejemplo anterior, se daría ese caso, ya que todos los alumnos de cuarto grado B, están incluidos en el conjunto B, de alumnos de cuarto grado.

Si dos conjuntos están formados por los mismos elementos se dice que son conjuntos iguales.

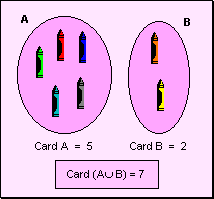
La unión de conjuntos es la suma de los elementos de dos conjuntos como se muestra en la primera imagen.

Fingermann, H. (4 de octubre de 2008). Concepto de conjunto. Deconceptos.com. Actualizado el 30 de marzo de 2023. https://deconceptos.com/matematica/conjunto